以下文章来源于香樟经济学术圈 ，作者胡惜玥
2022年9月30日，北京大学长聘副教授刘冲老师应邀作为主讲人，为在线参会者分享了“断点回归设计：方法与应用”的经济学训练课。
在本次课程中，刘冲老师从一个加州大学圣克鲁兹分校经济学系实施的GPA限制政策作为例子引入，对断点回归设计（RDD）的基本思想做了一个具体的阐释，总结了断点回归设计的优势和不足，之后又分析了两种断点回归设计的分析框架——基于连续性的分析框架和基于局部随机性的分析框架。老师对两种分析框架的基本理论假设都进行了详细的阐述，对于配置变量为离散变量的特殊情况也提供了解决办法，也举例子给大家展示了使用断点回归设计需要在论文中报告什么结果。
课程开始之初，刘冲老师先讲述了精确断点的基本思想。断点回归的核心思想是想要看断点附近的两组数据是否可以进行对比，找到可比样本，形成一个类似于反事实的对照组，在连续性样本中，断点回归设计要做的就是将断点左侧和右侧的曲线估计出来进行比较，通过样本点去拟合一条曲线，帮助我们判断在断点左右是否有跳跃。
断点回归设计的前提假设是：1.被观测对象不能操纵自己的配置变量来控制自己的处理状态。可以采用Stata软件中的rddensity命令来检验概率密度函数是否连续，但概率密度函数连续不意味着完全不存在操纵。2.断点附近的人群“可比”。为了验证是否“可比”，可以进行局部平滑性检验，确保除结果变量外，其它前定变量在断点附近不存在跳跃，研究者可以通过绘制散点图和拟合线呈现，也可以将其他前定变量作为结果变量，通过断点回归方法进行检验。但此时由于无法穷尽所有可能性，只能进行部分检验而不能进行全部检验，因而具有一定局限性。
因此，断点回归设计方法具有其优势和不足。其优势在于，断点回归设计的样本选择过程十分清晰，能够看见断点是由一个非常清晰的规则决定的，明确确定某些群体是被干预的个体，某些群体不是，因而断点回归设计比其他方法更接近随机实验，从实验基准中还原因果效应具有更强的因果推断力。同时，断点回归设计不需要特别强的假定，能够在较弱的假设下识别因果效应，同时它的假设易于检验。其不足在于，断点回归设计估计结果的外部有效性较差，估计的结果是“局部平均处理效应”（Local Average Treatment Effect, LATE），只能针对断点附近的群体做统一推断。
对于断点回归设计，拥有两种分析框架——基于连续性的断点回归设计框架和基于局部随机性的断点回归设计框架。在具体学习两种框架之前，首先需要了解断点回归设计的基本设定。
记配置变量（Assignment Variable）为X，配置变量的断点（Cutoff或Threshold）为c，个体的处理状态为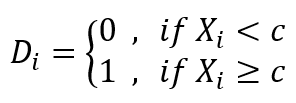
。研究者关注处理状态对潜在结果变量（Outcome Variable）Yi 影响。断点回归设计的两个前提假设是：1.位于断点c两侧、配置变量接近的个体间具备“可比性”。在基于连续性的RDD框架中，可比性指的是假设潜在结果变量须满足连续性。在基于局部随机性的RDD框架中，可比性指的则是断点附近需要满足类似于随机实验设计的条件。2.被观测对象不能通过操纵自己的配置变量来控制自己的处理状态。
基于连续性的RDD和基于局部随机性的RDD的差别在于：
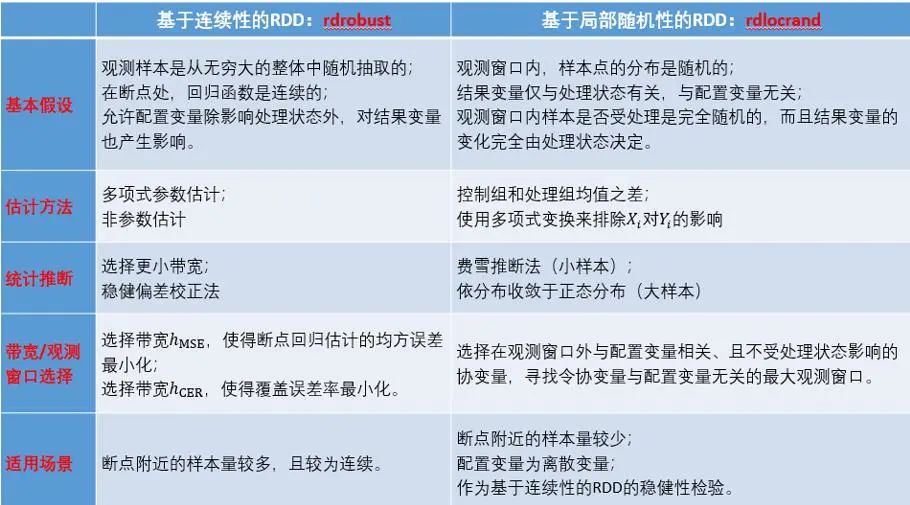
基于连续性的断点回归设计的基本假设是：1.用以分析的观测样本是从无穷大的整体中随机抽取的。2.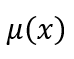
在断点处，是连续的。基于以上两种假设，对断点回归处理效应的估计也有分参数估计和非参数估计的不同估计方法。参数方法中，带宽ℎ和多项式阶数𝑝由研究者基于经验、研究问题特点和数据特性等情况事先给定。非参数方法中，给定阶数𝑝，带宽ℎ是通过MSE标准或CER标准等最优带宽选择标准得到的。
对于参数估计，通常使用局部多项式来估计未知的函数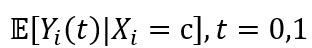
。局部多项式的拟合要先选择合适的多项式的阶数𝑝以及核函数𝐾(𝑥)。
对于非参数估计，带宽h决定了断点c两侧能够用以进行断点回归估计和推断的样本量。在早期的实证研究中,研究者往往根据先验知识事先设定带宽h，这在用局部多项式估计时比较常见。现在多用数据驱动的非参数方法进行选择，最常用的是带宽选择方法是MSE标准，即选择带宽hMSE，使得断点回归估计的均方误差（Mean Square Error, MSE）最小化。在构造估计的置信区间时，MSE可能存在一些偏差，更好的带宽选择方法是CER标准，即选择带宽hCER，使得覆盖误差率（Coverage Error Rate, CER）最小化。老师建议使用带宽hMSE对断点回归进行MSE最优点估计，然后选择使用相同的带宽hMSE或hCER使用来构建置信区间。
因此，在使用该方法时，需要在论文中报告系数的点估计值及其显著性、观测量N、带宽ℎ、多项式阶数𝑝、使用的核函数𝐾(𝑥)类型等，使用非参数方法时还需要报告带宽选择标准。此外，研究者需要进行以下几个步骤的工作：第一，通过绘制散点图和拟合线等方式观察结果变量在断点处是否存在跳跃；第二，使用rddensity命令检验配置变量的概率密度函数，判断配置变量是否被操纵；第三，进行局部平滑性检验，确认除结果变量外，其他前定协变量在断点附近不存在跳跃，研究者可以通过绘制散点图加以检验，也可以将其他前定协变量作为结果变量,通过断点回归方法进行检验；第四，选取虚拟断点进行安慰剂检验，如果虚拟断点处检验的结果是连续的,则能够更好地表明原断点的真实性。
基于局部随机性的断点回归设计适用于小样本研究或配置变量为离散值的情况，它的基本假设是：1.在观测窗口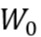
内，样本的分布函数
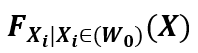已知，对所有样本点都相同，与结果变量
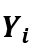无关，即分布函数可以被表示为
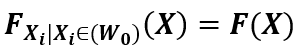。2.在观测窗口
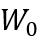内，配置变量
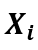仅通过处理状态影响结果变量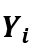，即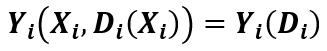
。假设2可以进行放松。
基于局部随机性的RDD估计使用费雪推断法，直观上看，该方法的含义是，假设处理效应不存在，则无论如何将观测窗口内的样本划分为处理组和控制组，两组的均值之差应当都相等（且为0）。如果实际的分组方法显著大于随机的分组方法，则表明实际上存在处理效应；反之亦然。
关键在于选择合适的观测窗口，在Stata中可以使用rdlocrand命令包中的rdwinselect命令来寻找最优观测窗口。使用满足两条要求的协变量Z确定观测窗口：1.协变量Z为前定变量，断点处的处理状态不会影响Z的取值，即有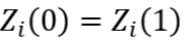
。2.至少某些观测的Z与X有相关性，观测窗口太大，处理组与控制组的X显著不同，使得两组的Z也产生显著差别，拒绝原假设
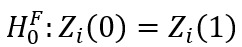。若配置变量为离散变量，通常选择最小的观测窗口，即断点两侧，距离断点最近的观测的取值。
在实证应用当中，需要汇报处理效应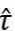
、原假设成立概率
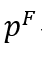、95%置信区间及观测窗口宽度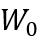。如果使用了协变量来确定观测窗口，还需要汇报不同观测窗口下对协变量进行费雪推断时原假设成立的概率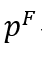。同时与之前类似，也需要进行前提假设检验与稳健性检验：第一，选择与处理状态无关的协变量，使用费雪推断法或直接画图来说明，在观测窗口内，处理组与控制组的协变量值没有显著差别；第二，检验观测窗口内，被观测对象能否通过操纵自己的配置变量来改变自己的处理状态，通常检验观测窗口内样本点的处理状态（0或1）是否符合成功概率为0.5的伯努利分布，如果不能拒绝符合成功概率为0.5的伯努利分布的原假设，则通过该检验；第三，在观测窗口外，选择虚拟断点和相同宽度的虚拟观测窗口，检验是否有处理效应，预期结果为没有处理效应；第四，选择宽度小于最优观测窗口的多个观测窗口，检验估计结果对观测窗口大小的敏感性。
在课程进行中，针对同学们提出的问题，刘老师也进行了耐心解答并分享了相关的论文和code，鼓励大家对这一方法进行更深一步学习，授课至此圆满结束。
来源：香樟经济学术圈
